
平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ
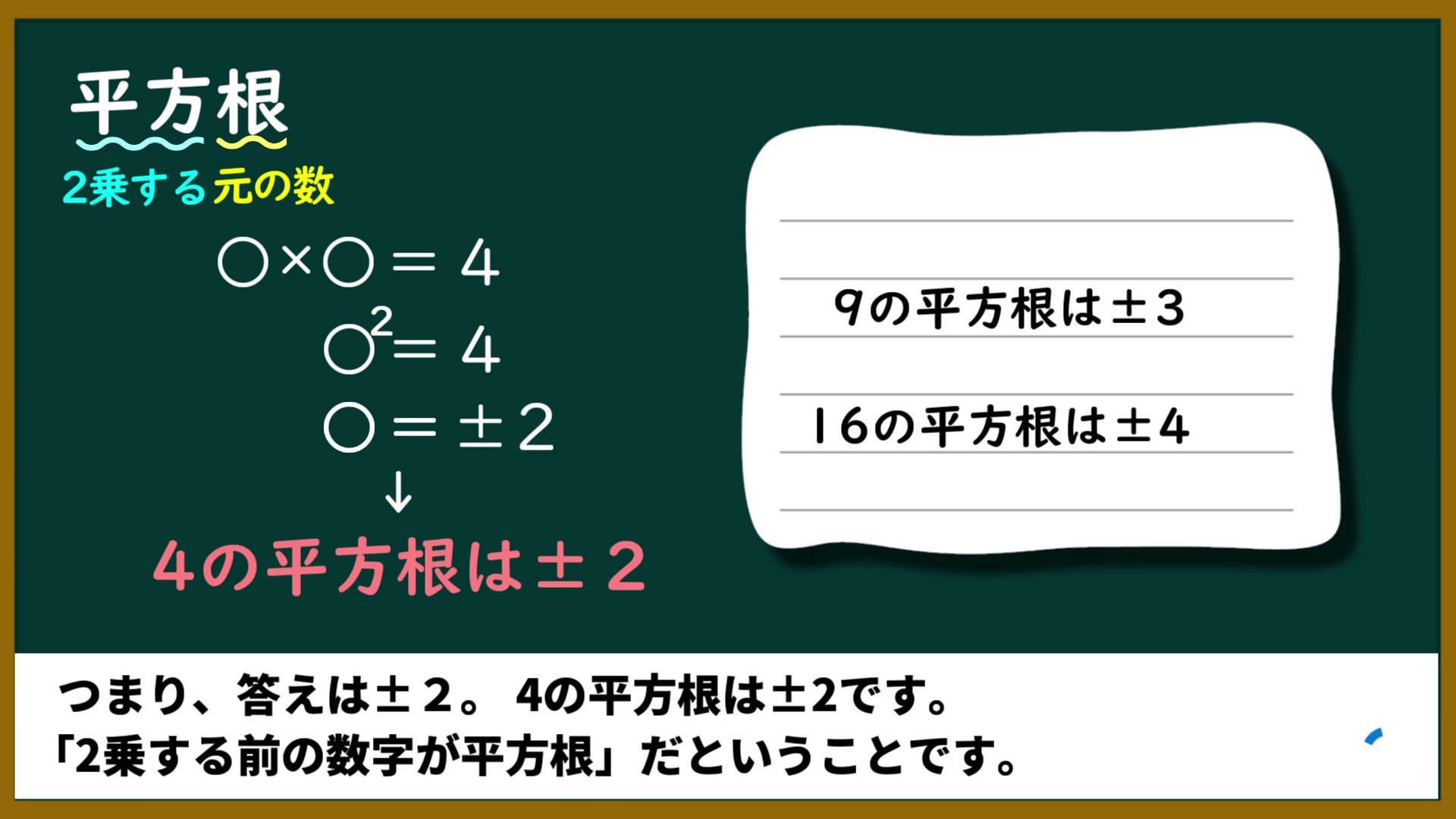
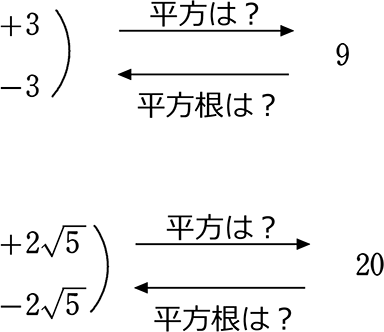
一方で数学では、累乗の逆があります。 平方根とは、ザックリと「累乗の逆」と理解しましょう。 2乗することで特定の数になる場合、平方根といいます。 4 2 の答えは前述の通り16です。では4の平方根は「+2」と「-2」 例えば、4の平方根で考えてみよう。 例 4の平方根を答えよう。 平方根とは、「 2乗する前の数 」のことをいうんだったね。 何を2乗すれば4になるかな? そう、2だ
4の平方根 とは
4の平方根 とは-平方根 練習問題 平方根(基礎) 素数と平方根(基礎) 平方根の計算(基礎) 平方根の計算2 平方根計算3 平方根計算4 平方根の大小など(基礎) 平方根問題7 平方根のおよその値 平方根計算5 平方根の大小 17年9月日 / 22年5月26日 このページでは、平方根の足し算・引き算・かけ算・割り算を4つのポイントに分けて解説していきます。 スポンサーリンク 目次 ①ルートの中身を

平方根の計算 ルートの掛け算の方法がわかる5つのステップ Qikeru 学びを楽しくわかりやすく
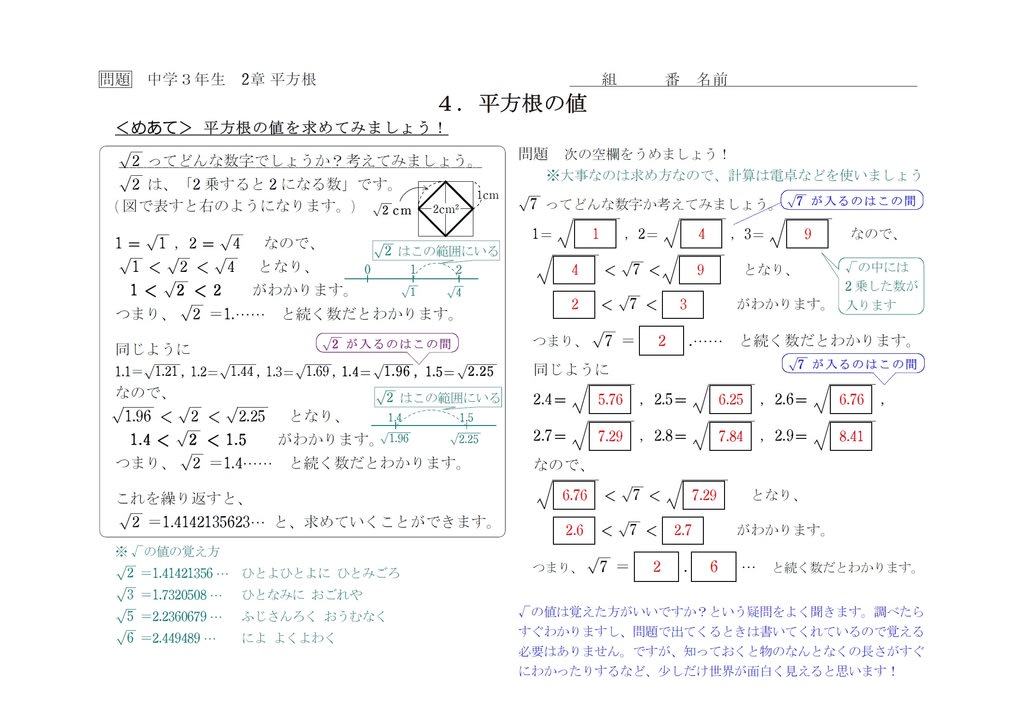
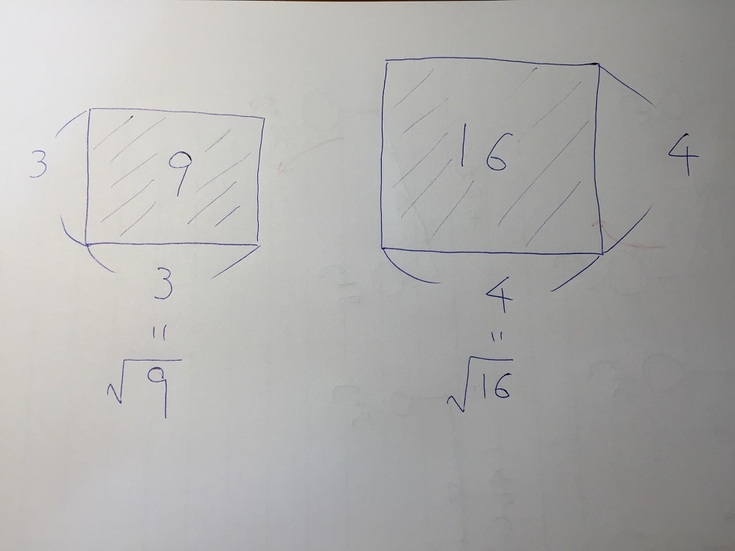
また、平方根を表す記号が「√(ルート)」です。 根号ともいいます。 今回は平方根の意味、ルート、求め方、覚え方、公式と問題について説明します。 根号の意味、根号の外し方は下記が参考に平方根とは? 平方根は、 「ある数 を2乗すると となるとき、その を の 平方根 という」 と定義されているものです。 文章を読むだけでは正直よくわかりませんね。 しかし、平方根の考え方自体 1.平方根って何? a、bという数字があったとして、a 2 =bを満たすaをbの 平方根 へいほうこん と呼びます。 二乗根 にじょうこん や 自乗根 じじょうこん とも呼びます。 a 2 とはa×a
じつは、平方根の意味とは、 2乗したら「ある数」になる数のこと なんだ。 この数を 「ある数」の平方根 とよんでいるんだ。 たとえば、25の平方根を考えてみよう。 平方根を考える 平方根とは 平方根とは、2乗してその数になる数のことを言います。 例えば、4の平方根は ± 4 と表し、 ± 2 となります。 また、5の平方根は ± 5 となります。 このように、平方根は正 8日撮影(22年 ロイター) 13日 ロイター ウクライナのゼレンスキー大統領は13日、ウクライナはロシア軍から奪還した4000平方キロメートルを
4の平方根 とはのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 平方根 2乗するとaになる数 教遊者 | 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 | 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 | 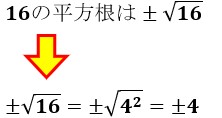 平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 | 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 | 平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 | 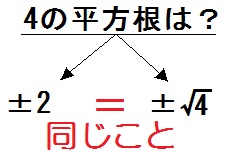 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 | 平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 | 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 | 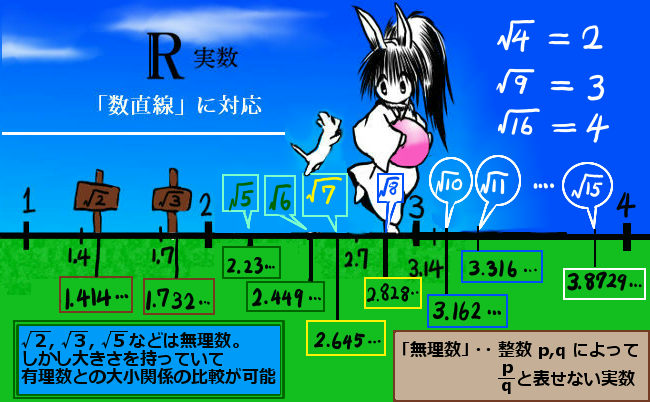 平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 | 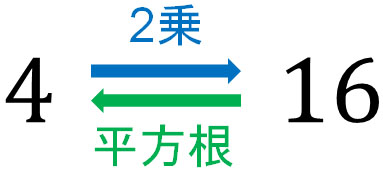 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
平方根 2乗するとaになる数 教遊者 | 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 | 平方根 2乗するとaになる数 教遊者 |
 平方根 2乗するとaになる数 教遊者 |  平方根 2乗するとaになる数 教遊者 |
4の平方根は2、というのは間違いと参考書に書いてありますが、どうしてでしょうか。また、√4=±2も誤りと書いてあります。 カルボキシ基coohはエステル結合coo を含んでい平方根 平方根ルートとは? 平方根の求め方を解説! 分数や小数の場合はどうやる? LINE 今回は中3で学習する平方根』の単元から この単元の基礎となる 平方根の求め方 について学んでいき
Incoming Term: 4の平方根 とは,




0 件のコメント:
コメントを投稿